Table Of Content
For fixed, random, and mixed models (balanced), the ANOVA table sums of squares calculations are identical. The only difference is with the expected mean squares, thus the test statistics. An advantage of the restricted mixed model is that 2 observations from the same random factor b level can be positively or negatively correlated. Orthogonal contrasts can be used to further partition the model sum of squares. There are many sets of orthogonal contrasts and thus, many ways to partition the sum of squares.
CRD in quality control analysis
The mean squares (\(MS\)) are sum of squares (\(SS\)) that arenormalized with the corresponding degrees of freedom. This is a so-calledone-way analysis of variance, or one-way ANOVA, because there isonly one factor involved. We now fit the model (2.4) using the function aov(which stands for analysis of variance). We state the model using the formulanotation where the response is listed on the left-hand side and the onlypredictor is on the right-hand side of the tilde sign “~”.
Randomized test-treatment studies with an outlook on adaptive designs - BMC Medical Research Methodology - BMC Medical Research Methodology
Randomized test-treatment studies with an outlook on adaptive designs - BMC Medical Research Methodology.
Posted: Tue, 01 Jun 2021 07:00:00 GMT [source]
Future applications and emerging fields for CRD
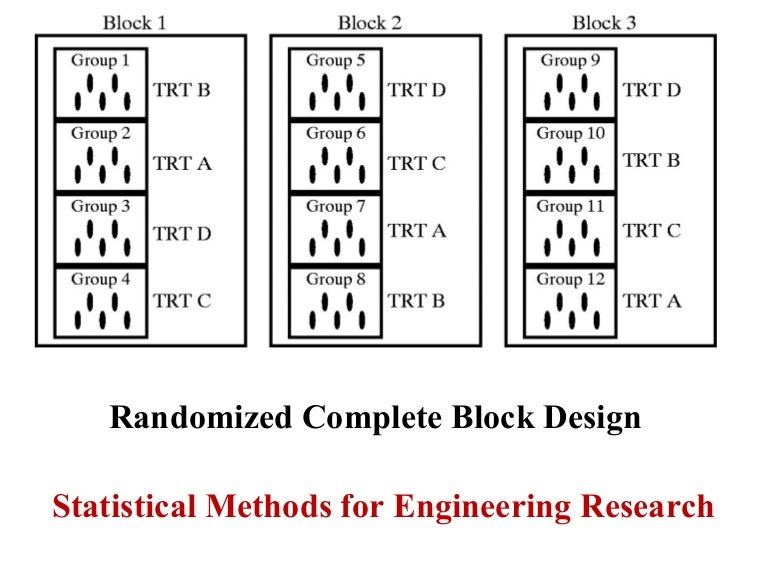
To make the coding a bit easier for this exercise, we will rename Population 7.5 to Population 1, Population 10.0 to Population 2, and Population 12.5 to Population 3. Randomly assign the five oat cultivars to each of the four blocks identified in the Treatments worksheet. The idea now is to create a random order of the treatments under the restriction that each Cultivar must occur once in each Block.
Selecting the independent variable
As a result, each experimental unit has an equal likelihood of receiving any specific treatment, ensuring a level playing field. Such random allocation is pivotal in eliminating systematic bias and bolstering the validity of experimental conclusions. Completely Randomized Design (CRD) is a research methodology in which experimental units are randomly assigned to treatments without any systematic bias. CRD gained prominence in the early 20th century, largely attributed to the pioneering work of statistician Ronald A. Fisher.
At its core, CRD is centered on harnessing randomness to achieve objective experimental outcomes. This approach effectively addresses unanticipated extraneous variables—those not included in the study design but that can still influence the response variable. In the context of CRD, these extraneous variables are expected to be uniformly distributed across treatments, thereby mitigating their potential influence. A completely randomized design is a type of experimental design where the experimental units are randomly assigned to the different treatments.
Use of research electronic data capture (REDCap) in a COVID-19 randomized controlled trial: a practical example ... - BMC Medical Research Methodology
Use of research electronic data capture (REDCap) in a COVID-19 randomized controlled trial: a practical example ....
Posted: Sat, 21 Aug 2021 07:00:00 GMT [source]

The code required to analyze the experiment is similar to what we used to analyze the Maize Population Example in the CRD activity. The linear additive model for an RCBD includes an additional term to account for the linear effect of blocks. In other words, you want to create a random order of the three populations (or treatments) within each block under the restriction that each population must occur once in each block.
Advantages of CRD
Even worse, such a p-value does not tell us wherethe actual problem is, how severe it is for the statistical inference and whatcould be done to fix it. Besides the estimated cell means in column emmean, we also get the corresponding95% confidence intervals defined through columns lower.CL and upper.CL. As we can see in the R output, group is a factor (a categorical predictor)having three levels, the reference level, which is the first level, is ctrl.
For example, in primary care settings, the randomization unit is often a doctor or a clinic (e.g., Dexter et al., 1998), where a number of patients belong to each doctor. In school settings, the randomization unit is often a classroom, where a number of students belong to each teacher (e.g., Ialongo et al., 1999). In CRT settings, individuals belonging to the same cluster are likely to resemble one another because of various factors such as common environment (e.g., clinic, classroom) and common deliverer of intervention treatment (e.g., doctor, teacher).
Given that, causal interpretation is possible with clarified assumptions, and sensitivity analysis is feasible if these assumptions are likely to be violated. Small numbers of clusters are often employed in psychosocial intervention trials, and therefore, the subsequent variance inflation is an important matter to be resolved. Further investigation is needed in this area to provide methods to improve the quality of standard error estimates given small numbers of clusters.
In the current article, we focus on how ignoring clustering affects the quality of CACE estimation and how considering both clustering and noncompliance improves its quality. How ignoring noncompliance affects the quality of ITT analysis and how considering both clustering and noncompliance improves its quality is dealt with in another manuscript (Jo, Asparouhov, & Muthén, in press). This article intends to promote an understanding of data clustering and noncompliance as simultaneous complications and to propose analyses that address both problems. In particular, the effect of intervention treatments on individuals who would abide by the intervention assignment (CACE) is the focus. Furthermore, this study employs a maximum-likelihood (ML) estimation method (built in Mplus Version 4 and higher; L. K. Muthén & Muthén, 1998–2007), which is more accessible to many applied researchers. Second, analytical complications from the simultaneous presence of noncompliance and data clustering are defined by extending the conventional notion of intraclass correlation (ICC).
The replications are just permutations of the different cakes heights respectively for A, B, C, D. Let’s see the above example in R language. Completely Randomized Design is also beneficial in quality control analysis, where ensuring the consistency of products is paramount. In academic discourse, while CRD is praised for its rigor and clarity, the effectiveness of the design relies heavily on the meticulous selection of the independent variable. Making this choice with thorough consideration ensures the research offers valuable insights with both academic and wider societal implications.

No comments:
Post a Comment